Kuratowski's closure-complement problem

In point-set topology, Kuratowski's closure-complement problem asks for the largest number of distinct sets obtainable by repeatedly applying the set operations of closure and complement to a given starting subset of a topological space. The answer is 14. This result was first published by Kazimierz Kuratowski in 1922.[1] The problem gained wide exposure three decades later as an exercise in John L. Kelley's classic textbook General Topology.[2]

Contents

Proof

Letting S denote an arbitrary subset of a topological space, write kS for the closure of S, iS for the interior of S, and cS for the complement of S. The following three identities imply that no more than 14 distinct sets are obtainable:

(1) kkS = kS

(2) ccS = S

(3) kckckckS = kckS.

The first two are trivial. The third follows from the identities kikiS = kiS and iS = ckcS.

A subset realizing the maximum of 14 is called a 14-set. The space of real numbers under the usual topology contains 14-sets. Here is one example:

(0,1)\cup(1,2)\cup\{3\}\cup\bigl([4,5]\cap\Q\bigr),

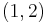where (1,2) denotes an open interval and [4,5] denotes a closed interval.

Further results

Despite its origin within the context of a topological space, Kuratowski's closure-complement problem is actually more algebraic than topological. A surprising abundance of closely related problems and results have appeared since 1960, many of which have little or nothing to do with point-set topology.[3]

References

  1. ^ [|Kuratowski, Kazimierz] (1922). "Sur l'operation A de l'Analysis Situs". Fundamenta Mathematicae (Warsaw: Polish Academy of Sciences) 3: 182–199. ISSN 0016-2736. http://www.docstoc.com/docs/54437805/On-the-Topological-Closure-Operation. 
  2. ^ [|Kelley, John] (1955). General Topology. Van Nostrand. p. 57. ISBN 0-387-90125-6. 
  3. ^ Hammer, P. C. (1960). "Kuratowski's Closure Theorem". Nieuw Archief voor Wiskunde (Royal Dutch Mathematical Society) 8: 74–80. ISSN 0028-9825. 

External links